Generating Bézier curve control points for regular stars

A more complete illustration suitable for printing is here. Illustrations and text kopyleft 2006 Chris Korda, all rites reversed.

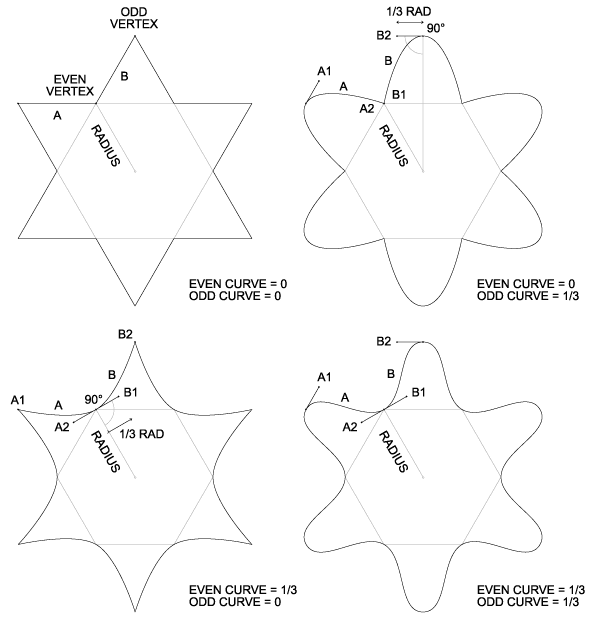
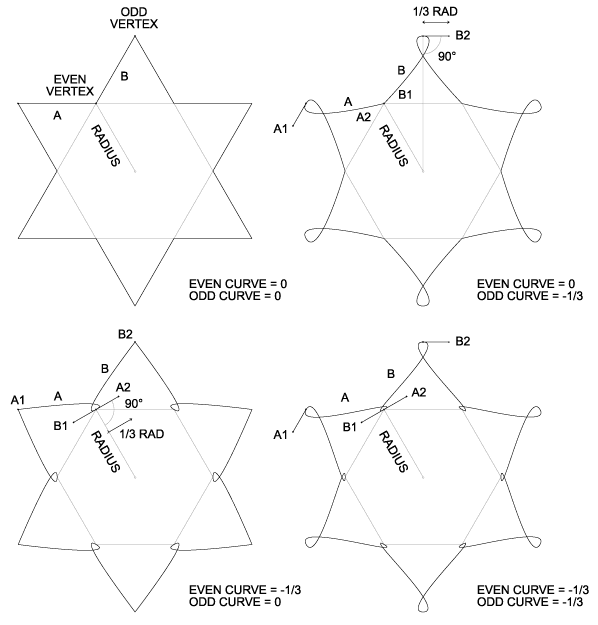
Background: A star is a regular polygon, but with an extra vertex between each normal vertex. The normal vertices are "even", while the extra vertices are "odd". By convention, the star's radius is the radius of any even vertex. The ratio of the odd radius to the even radius determines whether the star is convex (the points bulge outward) or concave (the points collapse inward), i.e. if odd_radius / even_radius > 1, the star is convex. For details, see: Star Factor.

Given a star as defined above, we would like to substitute curves for the usual line segments between each vertex. The end points of the curves are assumed to be the same as the end points of the line segments. The number of curves will be the same as the number of line segments, or N * 2, where N is the number of sides in the polygon from which the star is derived. The only remaining problem is, how to generate the two control points for each curve?

The solution must satisfy the following constraints:

1. The overal shape should be symmetrical, i.e. each star point should be identical to the others.
2. Each vertex have symmetrical curvature, i.e. for a given vertex, the curves on either side should be identical.
3. The curvature for odd vertices (the tips of the star points) should be controlled by one variable, while the curvature for even vertices (the inside corners, where the star points join) should be controlled by a second variable. Put another way, the points and inside corners should be grouped into two independently controllable curvatures.
4. Both odd and even curvatures should remain invariant with respect to the star's radius, i.e. inflating/deflating or zooming the star should not affect its curvature.
5. While both curvatures are non-zero, discontinuities (non-curved intersections) should not occur.

What unit should the curvature unit be in? By making it a fraction of the radius, constraint #4 can be satisfied trivially. For example, a curvature of 1 equals the radius, a curvature of .5 equals half the radius, etc.

The solution can be described as follows: For each vertex, draw a line tangent to the center of the star through the vertex. The two nearest control points (one for each neighboring curve) will lie along this line, and will be equidistant from the vertex. The distance from the vertex is given by the star's radius times the appropriate curvature (even or odd). Note that the curvature may be negative, in which the control points are reversed, causing the curves to loop in the opposite direction.

Assuming the star's vertices are already calculated, the above solution can be implementated relative easily. At each even vertex, two curves A and B intersect; the corresponding pair of curve control points A2 and B1 can be calculated as follows:

1. Construct a vector from the vertex to the center.
2. Scale the vector by the even curvature.
3. Rotate the vector 90 degrees around the vertex to get curve A's second control point (A2).
4. Rotate the vector -90 degrees around the vertex to get curve B's first control point (B1).

Since both rotations are 90 degrees, they can be accomplished via coordinate swapping instead of costly trig functions. Thus the solution can be reduced to one subtraction, four additions, and two multiplies, for each vertex. Note that constraint #3 (symmetrical curvature on both sides of each vertex) can be partially relaxed by scaling the A2 vector differently from the B1 vector, however if the constraint is abandoned entirely, the vectors are no longer necessarily tangent, and trig is unavoidable.

int CWhorldView::MakeCurves(const RING& rp, const DPOINT& Origin)
{
	int	sides = rp.Sides << 1;	// number of vertices
	int	points = sides * 3 + 2;	// one extra for duplicate control point
	CPoint	org(round(Origin.x), round(Origin.y));
	POINT	*pp = m_bpa;	// pointer to array of bezier points
	CPoint	pt, delta;
	float	curvature[2] = {rp.EvenCurve, float(rp.OddCurve / rp.StarRatio)};
	for (int i = 0; i < sides; i++) {
		pt = m_pa[i];	// next vertex
		delta = pt - org;	// construct vector from vertex to origin
		float	r = curvature[i & 1];	// odd or even curvature
		delta.x = round(delta.x * r);	// scale the vector
		delta.y = round(delta.y * r);
		*pp++ = CPoint(pt.x - delta.y, pt.y + delta.x);	// previous curve's 2nd control point
		*pp++ = pt;	// this curve's start point
		*pp++ = CPoint(pt.x + delta.y, pt.y - delta.x);	// this curve's 1st control point
	}
	*pp++ = m_bpa[0];	// copy final control point
	*pp++ = m_bpa[1];	// close the shape
	return(points - 1);	// skip first point: shape begins at m_bpa[1]
}